Minimax is a kind of backtracking algorithm that is used in decision making and game theory to find the optimal move for a player, assuming that your opponent also plays optimally.

• In Minimax the two players are called maximizer and minimizer.
• The maximizer tries to get the highest score possible while the minimizer tries to do the opposite and get the lowest score possible.

Every board state has a value associated with it.

• In a given state if the maximizer has upper hand then, the score of the board will tend to be some positive value.
• If the minimizer has the upper hand in that board state then it will tend to be some negative value.
• The values of the board are calculated by some heuristics which are unique for every type of game.

Since this is a backtracking based algorithm, it tries all possible moves, then backtracks and makes a decision.

A program to illustrate the Minimax Algorithm

A Tic-Tac-Toe example program to illustrate the Minimax Algorithm

function minimax(board, depth, isMaximizingPlayer):
 
  if current board state is a terminal state :
    return value of the board
 
  if isMaximizingPlayer :
    bestVal = -INFINITY 
    for each move in board :
      value = minimax(board, depth+1, false)
      bestVal = max( bestVal, value) 
    return bestVal
 
  else :
    bestVal = +INFINITY 
    for each move in board :
      value = minimax(board, depth+1, true)
      bestVal = min( bestVal, value) 
    return bestVal

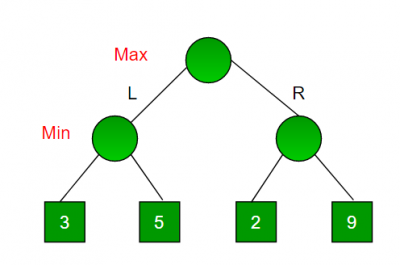
Consider a game which has 4 final states and paths to reach final state are from root to 4 leaves of a perfect binary tree as shown below.

• Assume you are the maximizing player and you get the first chance to move, i.e., you are at the root and your opponent at next level.
• Which move you would make as a maximizing player considering that your opponent also plays optimally?

Since this is a backtracking based algorithm, it tries all possible moves, then backtracks and makes a decision.

• Maximizer goes LEFT:
  • It is now the minimizers turn.
  • The minimizer now has a choice between 3 and 5.
  • Being the minimizer it will definitely choose the least among both, that is 3.
• Maximizer goes RIGHT:
  • It is now the minimizers turn.
  • The minimizer now has a choice between 2 and 9.
  • He will choose 2 as it is the least among the two values.

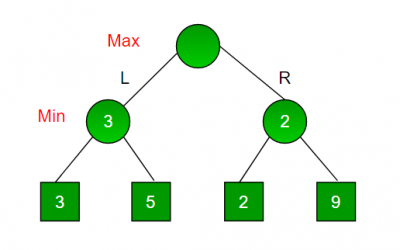
Being the maximizer you would choose the larger value that is 3.

• Hence the optimal move for the maximizer is to go LEFT and the optimal value is 3.

Now the game tree looks like below:

The above tree shows two possible scores when maximizer makes left and right moves.